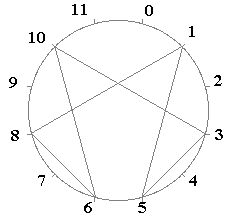
Ici, le but du jeu est de se rapprocher (mentalement) le plus possible de la forme optimale (6 clous et un seul fil) des fractions de n/ 7.
Cela n'est possible qu'avec les bases 3 et 5. (si l'on ne considère que les bases inférieures à 7),
Observons 1/ 7 en base 5 + 7n.
Pour les base de forme 5+7n,
la figure se parcourra dans le sens inverse
du sens utilisé par les bases de forme 3+7n.
|
|
1°chiffre |
2°chiffre |
3°chiffre |
4°chiffre |
5°chiffre |
6°chiffre |
|
|
n |
base |
||||||
|
0 |
5 |
0 |
3 |
2 |
4 |
1 |
2 |
|
1 |
12 |
1 |
8 |
6 |
10 |
3 |
5 |
|
2 |
19 |
2 |
13 |
10 |
16 |
5 |
8 |
|
3 |
26 |
3 |
18 |
14 |
22 |
7 |
11 |
|
. |
. |
. |
. |
. |
. |
. |
. |
|
n |
5+7n |
n |
3+5n |
2+4n |
4+6n |
1+2n |
2+3n |
Soit sous forme graphique:
n=1
1/7 en base 12 = (5 + 1x7)
1 - 8 - 6 - 10 - 3 - 5

et en résumé 1/7 en base 5+7n:
n __ 3+5n __ 2+4n __ 4+6n __ 1+2n __ 2+3n
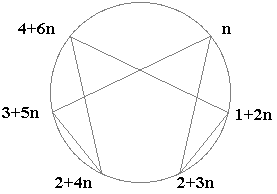
Comme on peut le voir, ces figures sont similaires et leurs différents points sont visités en sens inverse selon que la base est de forme 3+7n ou 5+7n.
3+7n et 5+7n sont les seules familles de bases générant de tels graphes pour le calcul de 1/7.
3x5=15 étant congru à 1 modulo 7 (il admet 1 pour reste dans la division par 7)
La plus petite base de la paire de famille, 3, est nommée génératrice de périodes invariantes pour le premier 7 et admet 5 comme base corrélée.
11 admet deux bases génératrices: 2 et 7 respectivement corrélées à 6 et 8. Les autres bases ne fournissant pas de telles périodes invariantes pour le premier 11.